Geometry¶
Classes:
|
Given an n_samples x n_dimensions array, compute pairwise or mean distances |
|
Get angle between line formed by two points and horizontal axis |
|
Compute absolute orientation (roll, pitch) from accelerometer and gyroscope measurements (eg from |
|
Rotate in 3 dimensions using |
|
Fit and transform 3d coordinates according to some spheroid. |
|
Order x-y coordinates into a line, such that each point (row) in an array is ordered next to its nearest points |
|
Given an ordered series of x/y coordinates (see |
Functions:
|
Ellipsoid equation for use with |
- class Distance(pairwise: bool = False, n_dim: int = 2, metric: str = 'euclidean', squareform: bool = True, *args, **kwargs)[source]¶
Bases:
TransformGiven an n_samples x n_dimensions array, compute pairwise or mean distances
- Parameters
pairwise (bool) – If False (default), return mean distance. if True, return all distances
n_dim (int) – number of dimensions (input array will be filtered like
input[:,0:n_dim]metric (str) – any metric acceptable to :func:`scipy.spatial.distance.pdist
squareform (bool) – if pairwise is True, if True return square distance matrix, otherwise return compressed distance matrix (dist(X[i], X[j] = y[i*j])
*args
**kwargs
Attributes:
Methods:
process(input)- format_in = {'type': <class 'numpy.ndarray'>}¶
- format_out = {'type': <class 'numpy.ndarray'>}¶
- class Angle(abs=True, degrees=True, *args, **kwargs)[source]¶
Bases:
TransformGet angle between line formed by two points and horizontal axis
Attributes:
Methods:
process(input)- format_in = {'type': <class 'numpy.ndarray'>}¶
- format_out = {'type': <class 'float'>}¶
- class IMU_Orientation(use_kalman: bool = True, invert_gyro: bool = False, *args, **kwargs)[source]¶
Bases:
TransformCompute absolute orientation (roll, pitch) from accelerometer and gyroscope measurements (eg from
hardware.i2c.I2C_9DOF)Uses a
timeseries.Kalmanfilter, and implements [PPT+18] to fuse the sensorsCan be used with accelerometer data only, or with combined accelerometer/gyroscope data for greater accuracy
- Parameters
invert_gyro (bool) – if the gyroscope’s orientation is inverted from accelerometer measurement, multiply gyro readings by -1 before using
use_kalman (bool) – Whether to use kalman filtering (True, default), or return raw trigonometric transformation of accelerometer readings (if provided, gyroscope readings will be ignored)
- Variables
kalman (
transform.timeseries.Kalman) – Ifuse_kalman == True, the Kalman Filter.
References
Methods:
process(accelgyro)- Parameters
accelgyro (tuple,
numpy.ndarray) -- tuple of (accelerometer[x,y,z], gyro[x,y,z]) readings as arrays, or
- process(accelgyro: Union[Tuple[ndarray, ndarray], ndarray]) ndarray[source]¶
- Parameters
accelgyro (tuple,
numpy.ndarray) – tuple of (accelerometer[x,y,z], gyro[x,y,z]) readings as arrays, or an array of just accelerometer[x,y,z]- Returns
filtered [roll, pitch] calculations in degrees
- Return type
numpy.ndarray
- class Rotate(dims='xyz', rotation_type='euler', degrees=True, inverse='', rotation=None, *args, **kwargs)[source]¶
Bases:
TransformRotate in 3 dimensions using
scipy.spatial.transform.Rotation- Parameters
dims (“xyz”) – string specifying which axes the rotation will be around, eg
"xy","xyz"`rotation_type (str) – Format of rotation input, must be one available to the
Rotationclass (but currently only euler angles are supported)degrees (bool) – whether to output rotation in degrees (True, default) or radians
inverse (“xyz”) – dimensions in the “rotation” input to
Rotate.process()to inverse before applying rotationrotation (tuple, list,
numpy.ndarray, None) – If supplied, use the same rotation for all processed data. If None,Rotate.process()will expect a tuple of (data, rotation).
Methods:
process(input)- Parameters
input (tuple,
numpy.ndarray) -- a tuple of (input[x,y,z], rotation[x,y,z]) where input is to be rotated
- process(input)[source]¶
- Parameters
input (tuple,
numpy.ndarray) – a tuple of (input[x,y,z], rotation[x,y,z]) where input is to be rotated according to the axes in rotation (indicated inRotate.dims). If only an input array is provided, a static rotation array must have been provided in the constructor (otherwise the most recent rotation will be used)- Returns
numpy.ndarray- rotated input array
- class Spheroid(target=(1, 1, 1, 0, 0, 0), source: tuple = (None, None, None, None, None, None), fit: Optional[ndarray] = None, *args, **kwargs)[source]¶
Bases:
TransformFit and transform 3d coordinates according to some spheroid.
Eg. for calibrating accelerometer readings by transforming them from their uncalibrated spheroid to the expected sphere with radius == 9.8m/s/s centered at (0,0,0).
Does not estimate/correct for rotation of the spheroid.
Examples
# Calibrate an accelerometer by transforming # readings to a 9.8-radius sphere centered at 0 >>> sphere = Spheroid(target=(9.8,9.8,9.8,0,0,0)) # take some readings... # imagine we're taking them from some sensor idk # say our sensor slightly exaggerates gravity # in the z-axis... >>> readings = np.array((0.,0.,10.5)) # fit our object (need >>1 sample) >>> sphere.fit(readings) # transform to proper gravity >>> sphere.process(readings) [0., 0., 9.8]
- Parameters
target (tuple) – parameterization of spheroid to transform to, if none is passed, transform to unit circle centered at (0,0,0). parameterized as:
(a, # radius of x dimension
b, # radius of y dimension c, # radius of z dimension x, # x-offset y, # y-offset z) # z-offset
source (tuple) – parameterization of spheroid to transform from in the same 6-tuple form as
target, if None is passed, assume we will useSpheroid.fit()fit (None,
numpy.ndarray) – Initialize with values to fit, if None assume fit will be called later.
References
Methods:
fit(points, **kwargs)Fit a spheroid from a set of noisy measurements
process(input)Transform input (x,y,z) points such that points in
sourceare mapped to those intargetgenerate(n[, which, noise])Generate random points from the ellipsoid
- fit(points, **kwargs)[source]¶
Fit a spheroid from a set of noisy measurements
updates the
_scaleand_offsetprivate arrays used to manipulate input dataNote
It’s usually important to pass
boundstoscipy.optimize.curve_fit()!!! passed as a 2-tuple of((min_a, min_b, ...), (max_a, max_b...))In particular such that a, b, and c are positive. If no bounds are passed, assume at least that much.- Parameters
points (
numpy.ndarray) – (M, 3) array of points to fit**kwargs () – passed on to
scipy.optimize.curve_fit()
- Returns
parameters of fit ellipsoid (a,b,c,x,y,z)
- Return type
- process(input: ndarray)[source]¶
Transform input (x,y,z) points such that points in
sourceare mapped to those intarget- Parameters
input (
numpy.ndarray) – x, y, and z coordinates- Returns
coordinates transformed according to the spheroid requested
- Return type
numpy.ndarray
- generate(n: int, which: str = 'source', noise: float = 0)[source]¶
Generate random points from the ellipsoid
- Parameters
n (int) – number of points to generate
which (‘str’) – which spheroid to generate from? (‘source’ - default, or ‘target’)
noise (float) – noise to add to points
- Returns
(n, 3) array of generated points
- Return type
numpy.ndarray
- _ellipsoid_func(fit, a, b, c, x, y, z)[source]¶
Ellipsoid equation for use with
Ellipsoid.fit()- Parameters
fit (
numpy.ndarray) – (M, 3) array of x,y,z points to fita (float) – X-scale parameter to fit
b (float) – Y-scale parameter to fit
c (float) – Z-scale parameter to fit
x (float) – X-offset parameter to fit
y (float) – Y-offset parameter to fit
z (float) – Z-offset parameter to fit
- Returns
result of ellipsoid function, minimize parameters to == 1
- Return type
- class Order_Points(closeness_threshold: float = 1, **kwargs)[source]¶
Bases:
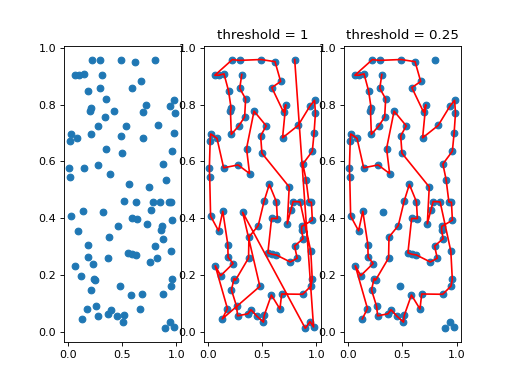
TransformOrder x-y coordinates into a line, such that each point (row) in an array is ordered next to its nearest points
Useful for when points are extracted from an image, but need to be treated as a line rather than disordered points!
Starting with a point, find the nearest point and add that to a deque. Once all points are found on the ‘forward pass’, start the initial point again goind the ‘other direction.’
The threshold parameter tunes the (percentile) distance consecutive points may be from one another. The default threshold of
1will connect all the points but won’t necessarily find a very compact line. Lower thresholds make more sensible lines, but may miss points depending on how line-like the initial points are.Note that the first point chosen (first in the input array) affects the line that is formed with the points do not form an unambiguous line. I am not surehow to arbitrarily specify a point to start from, but would love to hear what people want!
Examples
(Source code, png, hires.png, pdf)
- Parameters
closeness_threshold (float) – The percentile of distances beneath which to consider connecting points, from 0 to 1. Eg. 0.5 would allow points that are closer than 50% of all distances between all points to be connected. Default is 1, which allows all points to be connected.
Methods:
process(input)- Parameters
input (
numpy.ndarray) -- ann x 2array of x/y points
- class Linefit_Prasad(return_metrics: bool = False, **kwargs)[source]¶
Bases:
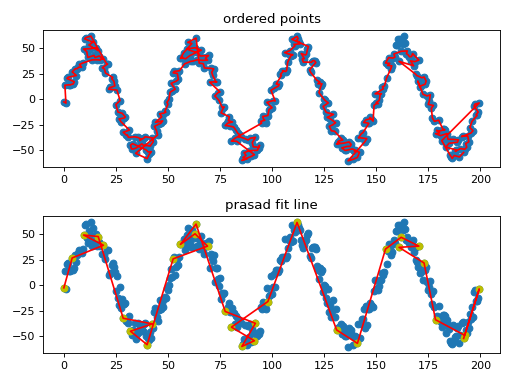
TransformGiven an ordered series of x/y coordinates (see
Order_Points), use D.Prasad et al.’s parameter-free line fitting algorithm to make a simplified, fitted line.Optimized from the original MATLAB code, including precomputing some of the transformation matrices. The attribute names are from the original, and due to the nature of code transcription doesn’t follow some of Autopilot’s usual structural style.
- Parameters
return_metrics (bool)
Examples
(Source code, png, hires.png, pdf)
References
[PQLC11] Original MATLAB Implementation: https://docs.google.com/open?id=0B10RxHxW3I92dG9SU0pNMV84alk
Methods:
process(input)Given an
n x 2array of ordered x/y points, return