Timeseries

Timeseries transformations, filters, etc.

Classes:

Filter_IIR([ftype, buffer_size, coef_type, axis])	Simple wrapper around scipy.signal.iirfilter()
Gammatone(freq, fs[, ftype, filtfilt, ...])	Single gammatone filter based on [Sla97]
Kalman(dim_state[, dim_measurement, dim_control])	Kalman filter!!!!!
Integrate([decay, dt_scale])

class Filter_IIR(ftype='butter', buffer_size=256, coef_type='sos', axis=0, *args, **kwargs)

Bases: Transform

Simple wrapper around scipy.signal.iirfilter()

Creates a streaming filter – takes in single values, stores them, and uses them to filter future values.

Parameters:

• ftype (str) – filter type, see ftype of scipy.signal.iirfilter() for available filters

• buffer_size (int) – number of samples to store when filtering

• coef_type ({‘ba’, ‘sos’}) – type of filter coefficients to use (see scipy.signal.sosfilt() and scipy.signal.lfilt())

• axis (int) – which axis to filter over? (default: 0 because when passing arrays to filter, want to filter samples over time)

• **kwargs – passed on to scipy.signal.iirfilter() , eg.

  • N - filter order

  • Wn - array or scalar giving critical frequencies

  • btype - type of band: ['bandpass', 'lowpass', 'highpass', 'bandstop']

Variables:

• coefs (np.ndarray) – filter coefficients, depending on coef_type

• buffer (collections.deque) – buffer of stored values to filter

• coef_type (str) – type of filter coefficients to use (see scipy.signal.sosfilt() and scipy.signal.lfilt())

• axis (int) – which axis to filter over? (default: 0 because when passing arrays to filter, want to filter samples over time)

• ftype (str) – filter type, see ftype of scipy.signal.iirfilter() for available filters

Methods:

process(input)

Filter the new value based on the values stored in Filter.buffer

process(input: float)

Filter the new value based on the values stored in Filter.buffer

Parameters:

input (float) – new value to filter!

Returns:

the filtered value!

Return type:

float

class Gammatone(freq: float, fs: int, ftype: str = 'iir', filtfilt: bool = True, order: int | None = None, numtaps: int | None = None, axis: int = -1, **kwargs)

Bases: Transform

Single gammatone filter based on [Sla97]

Thin wrapper around scipy.signal.gammatone !! (started rewriting this and realized they had made a legible version <3 ty scipy team, additional implementations in the references)

Examples

(Source code, png, hires.png, pdf)

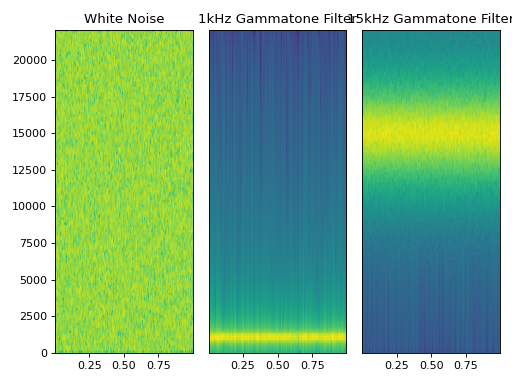
References

• [Sla97]

• Brian2hears implementation

• detly/gammatone

Parameters:

• freq (float) – Center frequency of the filter in Hz

• fs (int) – Sampling rate of the signal to process

• ftype (str) – Type of filter to return from scipy.signal.gammatone()

• filtfilt (bool) – If True (default), use scipy.signal.filtfilt(), else use scipy.signal.lfilt()

• order (int) – From scipy docs: The order of the filter. Only used when ftype='fir'. Default is 4 to model the human auditory system. Must be between 0 and 24.

• numtaps (int) – From scipy docs: Length of the filter. Only used when ftype='fir'. Default is fs*0.015 if fs is greater than 1000, 15 if fs is less than or equal to 1000.

• axis (int) – Axis of input signal to apply filter over (default -1)

• **kwargs – passed to scipy.signal.filtfilt() or scipy.signal.lfilt()

Methods:

process(input)

process(input: ndarray | list) → ndarray

class Kalman(dim_state: int, dim_measurement: int | None = None, dim_control: int = 0, *args, **kwargs)

Bases: Transform

Kalman filter!!!!!

Adapted from https://github.com/rlabbe/filterpy/blob/master/filterpy/kalman/kalman_filter.py simplified and optimized lovingly <3

Each of the arrays is named with its canonical letter and a short description, (eg. the x_state vector x_state is self.x_state

Parameters:

• dim_state (int) – Dimensions of the state vector

• dim_measurement (int) – Dimensions of the measurement vector

• dim_control (int) – Dimensions of the control vector

Variables:

• x_state (numpy.ndarray) – Current state vector

• P_cov (numpy.ndarray) – Uncertainty Covariance

• Q_proc_var (numpy.ndarray) – Process Uncertainty

• B_control (numpy.ndarray) – Control transition matrix

• F_state_trans (numpy.ndarray) – State transition matrix

• H_measure (numpy.ndarray) – Measurement function

• R_measure_var (numpy.ndarray) – Measurement uncertainty

• M_proc_measure_xcor (numpy.ndarray) – process-measurement cross correlation

• z_measure (numpy.ndarray) –

• K (numpy.ndarray) – Kalman gain

• y (numpy.ndarray) –

• S (numpy.ndarray) – System uncertainty

• SI (numpy.ndarray) – Inverse system uncertainty

• x_prior (numpy.ndarray) – State prior

• P_prior (numpy.ndarray) – Uncertainty prior

• x_post (numpy.ndarray) – State posterior probability

• P_post (numpy.ndarray) – Uncertainty posterior probability

References

Roger Labbe. “Kalman and Bayesian Filters in Python” - https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python Roger Labbe. “FilterPy” - https://github.com/rlabbe/filterpy

Methods:

predict([u, B, F, Q])	Predict next x_state (prior) using the Kalman filter x_state propagation equations.
update(z[, R, H])	Add a new measurement (z_measure) to the Kalman filter.
process(z, **kwargs)	Call predict and update, passing the relevant kwargs
residual_of(z)	Returns the residual for the given measurement (z_measure).
measurement_of_state(x)	Helper function that converts a x_state into a measurement.

Attributes:

alpha

Fading memory setting.

predict(u=None, B=None, F=None, Q=None)

Predict next x_state (prior) using the Kalman filter x_state propagation equations.

Update our state and uncertainty priors, x_prior and P_prior

Parameters

unp.array, default 0

Optional control vector.

Bnp.array(dim_state, dim_u), or None

Optional control transition matrix; a value of None will cause the filter to use self.B_control.

Fnp.array(dim_state, dim_state), or None

Optional x_state transition matrix; a value of None will cause the filter to use self.F_state_trans.

Qnp.array(dim_state, dim_state), scalar, or None

Optional process noise matrix; a value of None will cause the filter to use self.Q_proc_var.

update(z: ndarray, R=None, H=None) → ndarray

Add a new measurement (z_measure) to the Kalman filter.

If z_measure is None, nothing is computed. However, x_post and P_post are updated with the prior (x_prior, P_prior), and self.z_measure is set to None.

Parameters:

• z (numpy.ndarray) – measurement for this update. z_measure can be a scalar if dim_measurement is 1, otherwise it must be convertible to a column vector.

  If you pass in a value of H_measure, z_measure must be a column vector the of the correct size.

• R (numpy.ndarray, int, None) – Optionally provide R_measure_var to override the measurement noise for this one call, otherwise self.R_measure_var will be used.

• H (numpy.ndarray, None) – Optionally provide H_measure to override the measurement function for this one call, otherwise self.H_measure will be used.

process(z, **kwargs)

Call predict and update, passing the relevant kwargs

Parameters:

• z ()

• **kwargs ()

Returns:

self.x_state

Return type:

np.ndarray

residual_of(z)

Returns the residual for the given measurement (z_measure). Does not alter the x_state of the filter.

measurement_of_state(x)

Helper function that converts a x_state into a measurement.

Parameters

xnp.array

kalman x_state vector

Returns

z_measure(dim_measurement, 1): array_like

measurement for this update. z_measure can be a scalar if dim_measurement is 1, otherwise it must be convertible to a column vector.

property alpha

Fading memory setting. 1.0 gives the normal Kalman filter, and values slightly larger than 1.0 (such as 1.02) give a fading memory effect - previous measurements have less influence on the filter’s estimates. This formulation of the Fading memory filter (there are many) is due to Dan Simon [1]_.

class Integrate(decay=1, dt_scale=False, *args, **kwargs)

Bases: Transform

Methods:

process(input)

process(input)